OpenFOAM – FOURTH ATTEMPT. AIR FLOW THROUGH A SUGAR BEET CLAMP w BETTER GUESSES FOR DARCY & FORCHHEIMER

!!!!!

THE VALUE USED FOR KINEMATIC VISCOSITY IN THE SIMULATION THAT IS DESCRIBED IN THIS POST WAS INCORRECT. THE DARCY-FORCHHEIMER COEFFICIENTS, HOWEVER, DO SEEM TO BE CORRECT. FOR AN UPDATED ON THE RESULTS IS AVAILABLE

!!!!!

In 2003, Lope G. Tabil and three co-authors decided that they would make my 2021 life much much easier by publishing the paper Airflow Resistance of Sugarbeet. This paper reports some very useful values for the fluid dynamic properties of piles of sugar beets. I’m not sure where they saw their work going, but my feeling is that a model such as mine was probably within their realms of imagination. So, thank you Prof. Tabil and friends.

From their work, it is possible to derive accurate estimates for the Darcy (D) and the Forchheimer (F) coefficients. For one of the experimental conditions they ran, I came up with values of around 500 000 and 300, respectively. Using these and two other sets of values in the model I’ve been developing, the result, after 250 iterations for each version (convergence wasn’t reached, but it was oh so close):

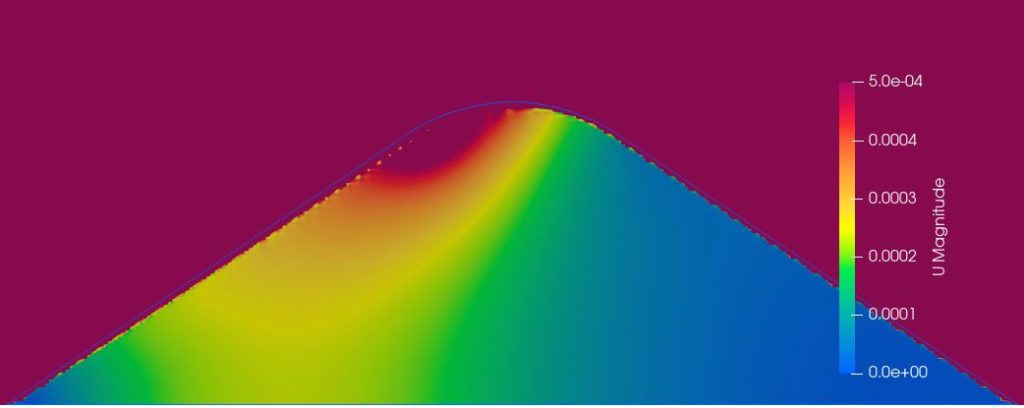
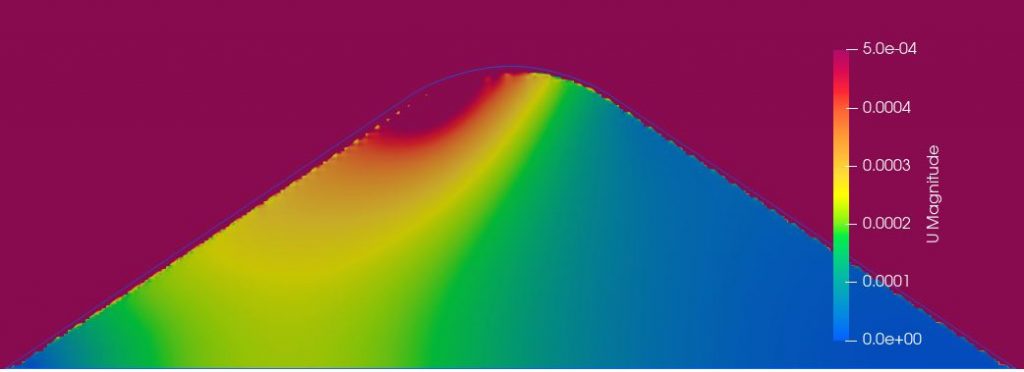
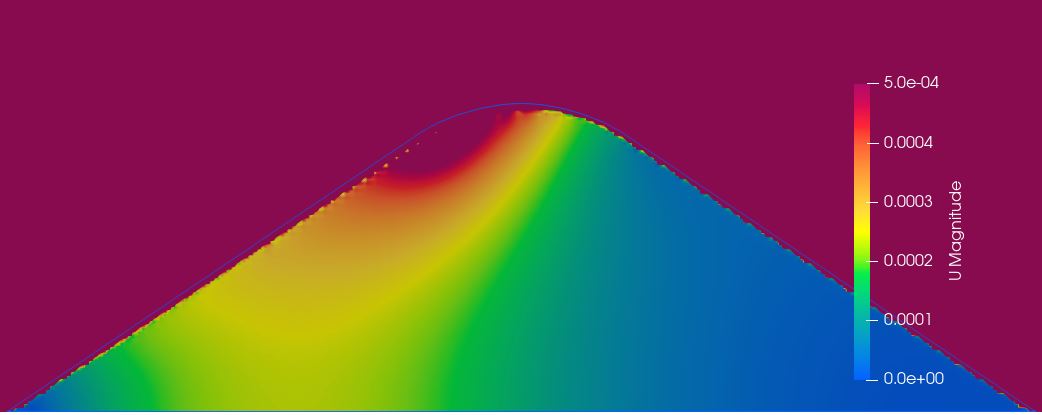
The image on the left uses parameters taken from a test with only large beets (>1200g) and 0% foreign material in the sample. The middle image uses parameters from small beets (<1200g) and 0% foreign material, and is nearly indistinguishable from the Large-0% setup. Looking at the parameters, this isn’t a surprise – they are only about 5% different on the Darcy coefficient. The image on the right, with beets of mixed size and 8.5% foreign material, shows much less movement of air. With both the D and F over double that of the Large-0% case, it’s not a surprise. There is data for a Mixed-0% case and it has much lower D, but comparable F values to the other 0% foreign material cases. This suggests that it is the foreign material causing the drop in air flow, not the beet size.

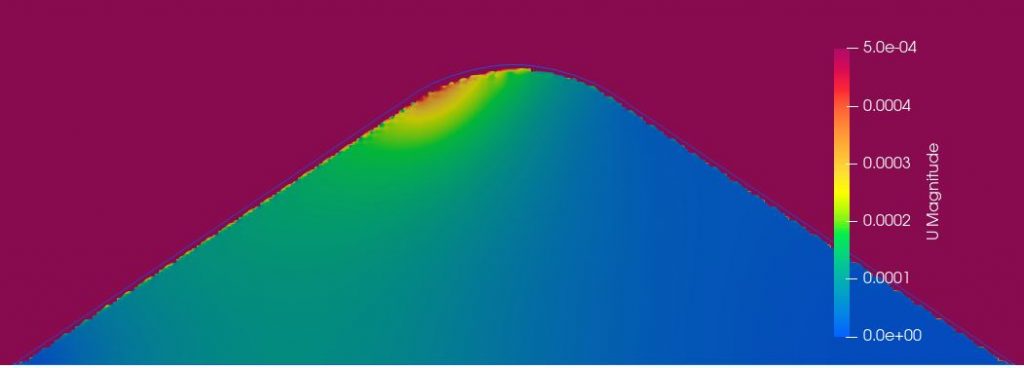
Zooming in on the version with the large beets and 0% foreign material:

Overall, I’m not convinced – these air velocities seem too little. But I might be wrong. The clear difference in air velocity between the two sides of the clamp reflects what we’ve seen in measuring temperature in clamps – that the wind direction is very important for the rate of temperature change in the clamp.

Comparing these results to something similar suggests that the results are at the bottom end of the realm of possibilities. The mine pile example has a similar ambient air velocity around a much larger and less porous pile and gets velocity values of a maximum 0.001m/s (similar to the maximums seen here). I would expect a lot more air flow through a pile of sugar beets than a pile of small rocks. An example of large (ca. 1/4 tonne?) bins of apples in a store room found air flow rates around 0.02 to 0.2m/s in the middle of the bins when the air velocity around the bins was between 0.8 and 1.4m/s. The variation came with the height of the bin in the store room. The air wasn’t forced through these bins, like it would be in wind tunnel experiment like Tabil’s, but it would still be more forced than in the open field. Also the bins were only 100cm (W) x 120cm (D) x 78cm (H). Conversely, these bins were only 7% open on their sides.

If the model is right, I’m going to have a very hard time measuring and verifying it. I don’t think many air sensors are good at measuring 0.0001 m/s. I’m hoping to build smoke detectors into my measuring devices to see if we can time how long smoke takes to reach into the clamp. At an average of 0.0002m/s and 6m into the clamp, that should be 30 000 seconds/ 500 minutes/ 8 hours and 20 minutes. At the other end, with an average of 0.00035m/s and 2m into the clamp, that’s 5,714 seconds/ 95 minutes/ 1 hour and 35 minutes. That’s a lot of smoke bombs…

If my hunch is right and the model is wrong, then I am also wrong – I created the model. I have no reason to suspect any issues with the work of Tabil et al., so if the model is wrong, then I have done some wrong calculations along the way. My first point to check will be to see if I’ve calculated and used the Darcy and Forchheimer coefficients in the correct way. Maybe I’ve missed a decimal point somewhere…

REFERENCES:

Amos, R. T., et al. (2009). “Measurement of Wind-Induced Pressure Gradients in a Waste Rock Pile.” Vadose Zone Journal 8(4): 953-962.

Praeger, U., et al. (2020). “Airflow distribution in an apple storage room.” Journal of Food Engineering 269.

Tabil, L. G., et al. (2003). “Thermal Properties of Sugarbeet Roots.” Journal of Sugar Beet Research 40: 209-228.